How does binding energy per nucleon affect the stability of a nucleus: Nuclear stability and nuclear forces depend on binding energy, mass defect and nuclear binding energy, relative stability of isotopes and binding energy, nuclear energy examples.
Page Contents
 How does binding energy per nucleon affect the stability of a nucleus
How does binding energy per nucleon affect the stability of a nucleus
Nucleus: Nucleus is found to be a source of tremendous amount of energy which utilizes for the destructive and constructive purpose. Hence the study of nucleus of an atom has become so important. That it gives a separate branch of chemistry under the heading of Nuclear Chemistry.
The nucleus occupies the central space in the atom. All the mass of an atom is concentrated in the nucleus. Nucleus has a radius of only about 10-15 m, the density of nucleus is enormous. Above 1012 times that of lead.
The products of efferent nuclear reactions detect About 20 different particles. It regards that nucleus derives from neutron in the following way.
Neutron → Proton + Electron
Internal stress produces photons within the Nucleus.
Nuclear Forces: The radius of nucleus is small (≈ 10-15 m). It finds two protons lying in the nucleu to repel each other with an electrostatic force of about 6 tones. The question arises how such a large number of protons present in such a tiny space without repulsion.
The stronger proton-neutron, neutron-neutron and even proton-proton attractive forces exist in the nucleus. These attractive forces are called nuclear forces. Nuclear forces 1021 times stronger than electrostatic forces. The nuclear force operate only within mall distance of about 1 X 10-15 m. Drop to zero at a distance of 14 x 10-12 m. Hence theses are referred to short range forces.
Nuclear Stability
Anyone of the following may discusses the stability of Nucleus.
 1 a.m.u.= 931.5 MeV = 1.66 x 10-27 kg = 1.492 x 10-10 J = 3.564 x 10-11 cal.
1 a.m.u.= 931.5 MeV = 1.66 x 10-27 kg = 1.492 x 10-10 J = 3.564 x 10-11 cal.
Mass defect and Nuclear binding energy
The most acceptable theory about the atomic nuclear stability based upon the fact. That the observed atomic mass of all known isotopes (except hydrogen) is always less from the sum of the weights of protons and neutrons. And electrons present in it. Consider the case of helium having 2 protons and neutrons and 2 electrons.
| Mass of 2 electrons | 2 x 0.000543 | 0.001086 a.m.u. |
| Mass of 2 protons | 2 x 1.00758 | 2.01516 a.m.u. |
| Mass of 2 neutrons | 2 x 1.00893 | 2.01786 a.m.u. |
Expected mass of helium = 4.03410 a.m.u.
The actual mass of helium = 4.00390 a.m.u.
Deference between the expected mass and the actual mass of helium
Δm = 4.03410 – 4.00390 a.m.u.
Mass Defect: The difference between the expected mass and actual mass of an isotope called mass defect. it denotes by Δm.
Binding Energy
The natural question i that where this mass has gone? The suggestion is that this mass converted to energy which released in the formation of the given nucleus from individual protons and neutrons. The released of energy results for in the stability of the nucleus.
it help in binding the nucleus together and hence it called Binding Energy. Thus binding energy of a nucleus may define as the amount of energy released during the formation of a hypothetical nucleus from its protons and neutrons.
Mathematically, binding energy can calculate from Einstein Equation,
E = Δ mc2
Where Δm is the mass lost, i.e. mass defect and c is the velocity of light (3 x 108 m/sec)
Binding energy = Δm x 931.5 MeV
This is because 1 a.m.u. = 931.5 MeV
Thus the binding energy of helium nucleus = Δm x 931.5 MeV = 0.0302 x 931.5 MeV = 28.14 MeV
It Δm is in gram, E will be in MeV per gm atom. Note: Nucleus dimension express in Fermi unit. (1 Fermi = 10-13 cm)
Greater the mass defect , greater is binding energy of the nucleus.
The binding energy of a nucleus when divided by the number of nucleus gives the mean binding energy per nucleus. Thus the mean binding energy per nucleon of helium is
= 28.14/4 = 7.03 MeV
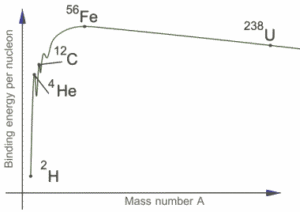
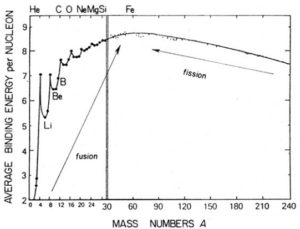
The binding energy per nucleon is a measure of the stability of the nucleus.The greater the binding energy per nucleon, the more stable is the nucleus.
The isotopes with intermediate mass number 40 to 100 are mot stable. The elements with low mass number or high mass number tend to become stable by acquiring intermediate mass number.
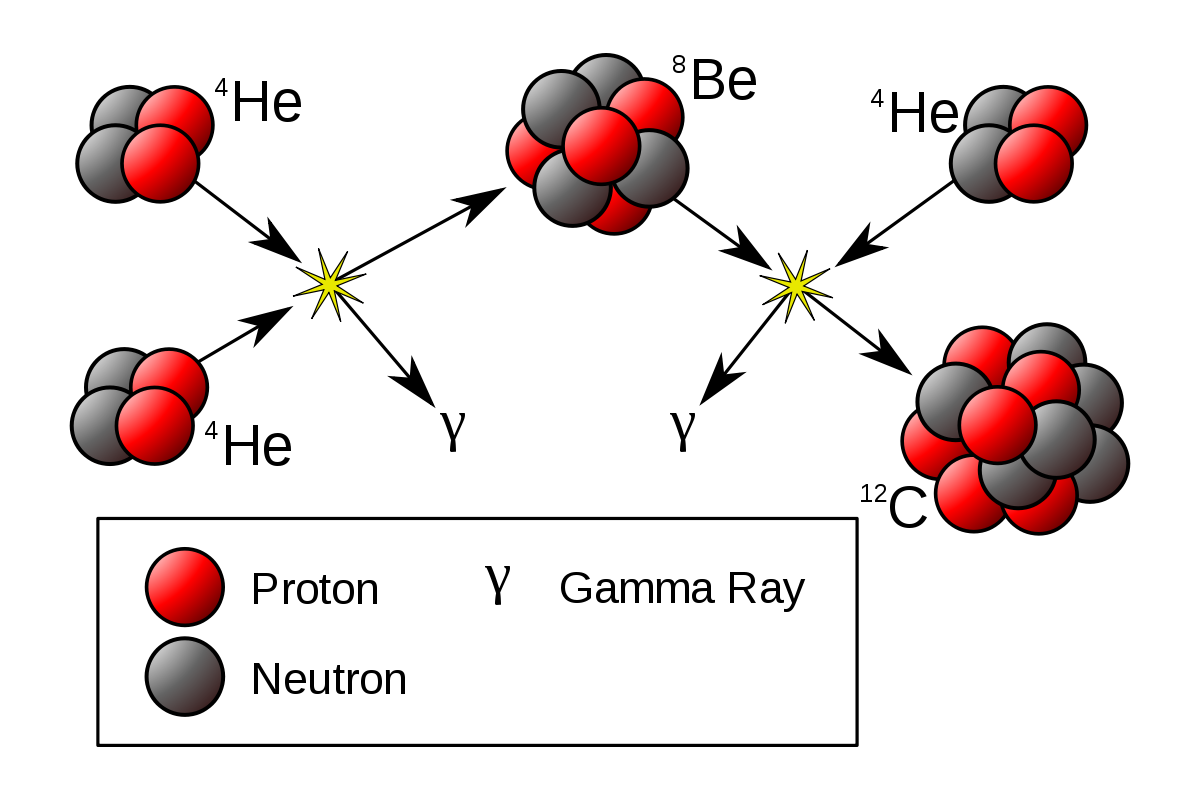
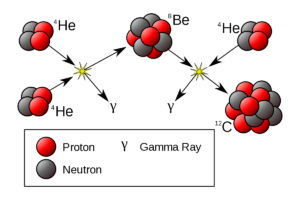
Nuclei of lighter elements combine together to form a heavier nucleus of intermediate mass number. While the nuclei of heavy elements splits into two lighter nuclei of intermediate mass number (nuclear fusion).
Relative stability of isotopes and binding energy
Value of binding energy predicts the relative stability of different isotopes of an element. If the value of binding energy is negative, the product nucleus or nuclei will be less stable than the reactant nuclei or nucleus. But if the binding energy is positive the product of nucleus is more stable than the reactant nucleus. Thus the relative stability of the different isotope of an element can predicted by the value of binding energy for each successive addition of one neutron to the nucleus.
2He3 + 0n1 ⇒ 2He4 + 20.5 MeV
2He4 + 0n1 ⇒ 2He5 – 0.8 MeV
Therefor 2He4 is more stable than 2He3 and 2He5 .
Example:-
Calculate the energy released in joules and MeV in the following nuclear reaction.
1He2 + 1He2 → 2He3 + 0n1
Solution: Assume that the mases of 1He2, 2He3 and (n) are respectively 2.0141, 3.0160 and 1.0087 in amu.
Mass of the reactants = 2 x 2.0141 amu = 4.0282 amu
Mass of products = 3.0160 + 1.0087 amu = 4.0247 amu
∴ Δm = 4.0282 – 4.0247 amu = 0.0035 amu = 3.5 x 10-3 amu
∴ ΔΕ = 3.5 x 10-3 x 931 MeV = 3.260 MeV
or ΔΕ = 3.260 x 1.602 x 10-19 x 106 J = 5.223 x 10-23 J
Repeat:
Nucleus: Nucleus is found to be a source of tremendous amount of energy which utilizes for the destructive and constructive purpose. Hence the study of nucleus of an atom has become so important. That it gives a separate branch of chemistry under the heading of Nuclear Chemistry.
The nucleus occupies the central space in the atom. All the mass of an atom is concentrated in the nucleus. Nucleus has a radius of only about 10-15 m, the density of nucleus is enormous. Above 1012 times that of lead.
The products of efferent nuclear reactions detect About 20 different particles. It regards that nucleus derives from neutron in the following way.
Neutron → Proton + Electron
Internal stress produces photons within the Nucleus.
Nuclear Forces: The radius of nucleus is small (≈ 10-15 m). It finds two protons lying in the nucleu to repel each other with an electrostatic force of about 6 tones. The question arises how such a large number of protons present in such a tiny space without repulsion.
The stronger proton-neutron, neutron-neutron and even proton-proton attractive forces exist in the nucleus. These attractive forces are called nuclear forces. Nuclear forces 1021 times stronger than electrostatic forces. The nuclear force operate only within mall distance of about 1 X 10-15 m. Drop to zero at a distance of 14 x 10-12 m. Hence theses are referred to short range forces.
Nuclear Stability
Anyone of the following may discusses the stability of Nucleus.
 1 a.m.u.= 931.5 MeV = 1.66 x 10-27 kg = 1.492 x 10-10 J = 3.564 x 10-11 cal.
1 a.m.u.= 931.5 MeV = 1.66 x 10-27 kg = 1.492 x 10-10 J = 3.564 x 10-11 cal.
Mass defect and Nuclear binding energy
The most acceptable theory about the atomic nuclear stability based upon the fact. That the observed atomic mass of all known isotopes (except hydrogen) is always less from the sum of the weights of protons and neutrons. And electrons present in it. Consider the case of helium having 2 protons and neutrons and 2 electrons.
| Mass of 2 electrons | 2 x 0.000543 | 0.001086 a.m.u. |
| Mass of 2 protons | 2 x 1.00758 | 2.01516 a.m.u. |
| Mass of 2 neutrons | 2 x 1.00893 | 2.01786 a.m.u. |
Expected mass of helium = 4.03410 a.m.u.
The actual mass of helium = 4.00390 a.m.u.
Deference between the expected mass and the actual mass of helium
Δm = 4.03410 – 4.00390 a.m.u.
Mass Defect: The difference between the expected mass and actual mass of an isotope called mass defect. it denotes by Δm.
Binding Energy
The natural question i that where this mass has gone? The suggestion is that this mass converted to energy which released in the formation of the given nucleus from individual protons and neutrons. The released of energy results for in the stability of the nucleus.
it help in binding the nucleus together and hence it called Binding Energy. Thus binding energy of a nucleus may define as the amount of energy released during the formation of a hypothetical nucleus from its protons and neutrons.
Mathematically, binding energy can calculate from Einstein Equation,
E = Δ mc2
Where Δm is the mass lost, i.e. mass defect and c is the velocity of light (3 x 108 m/sec)
Binding energy = Δm x 931.5 MeV
This is because 1 a.m.u. = 931.5 MeV
Thus the binding energy of helium nucleus = Δm x 931.5 MeV = 0.0302 x 931.5 MeV = 28.14 MeV
It Δm is in gram, E will be in MeV per gm atom. Note: Nucleus dimension express in Fermi unit. (1 Fermi = 10-13 cm)
Greater the mass defect , greater is binding energy of the nucleus.
The binding energy of a nucleus when divided by the number of nucleus gives the mean binding energy per nucleus. Thus the mean binding energy per nucleon of helium is
= 28.14/4 = 7.03 MeV
The binding energy per nucleon is a measure of the stability of the nucleus.The greater the binding energy per nucleon, the more stable is the nucleus.
The isotopes with intermediate mass number 40 to 100 are mot stable. The elements with low mass number or high mass number tend to become stable by acquiring intermediate mass number.
Nuclei of lighter elements combine together to form a heavier nucleus of intermediate mass number. While the nuclei of heavy elements splits into two lighter nuclei of intermediate mass number (nuclear fusion).
Value of binding energy predicts the relative stability of different isotopes of an element. If the value of binding energy is negative, the product nucleus or nuclei will be less stable than the reactant nuclei or nucleus. But if the binding energy is positive the product of nucleus is more stable than the reactant nucleus. Thus the relative stability of the different isotope of an element can predicted by the value of binding energy for each successive addition of one neutron to the nucleus.
2He3 + 0n1 ⇒ 2He4 + 20.5 MeV
2He4 + 0n1 ⇒ 2He5 – 0.8 MeV
Therefor 2He4 is more stable than 2He3 and 2He5 .
Example:-
Calculate the energy released in joules and MeV in the following nuclear reaction.
1He2 + 1He2 → 2He3 + 0n1
Solution: Assume that the mases of 1He2, 2He3 and (n) are respectively 2.0141, 3.0160 and 1.0087 in amu.
Mass of the reactants = 2 x 2.0141 amu = 4.0282 amu
Mass of products = 3.0160 + 1.0087 amu = 4.0247 amu
∴ Δm = 4.0282 – 4.0247 amu = 0.0035 amu = 3.5 x 10-3 amu
∴ ΔΕ = 3.5 x 10-3 x 931 MeV = 3.260 MeV
or ΔΕ = 3.260 x 1.602 x 10-19 x 106 J = 5.223 x 10-23 J
Thanking you for visiting and reading the post ‘How does binding energy per nucleon affect the stability of a nucleus’. If you like the post then comment in the comment box and share this post in Facebook, twitter or Google.
Get Reference click here